Multiplication Worksheets

I think last time I posted I said I’d be posting more often, so I feel like I need to point out that once a month is “more often” than once a year. So if you were expecting to come here every week I’m a little bit sorry to have disappointed you.

One of the reasons I wanted to learn how to make math resources for myself is because I never quite like the things that are available to me on the Internet. I mean, they’re okay I guess, but I usually end up feeling like they could have been more interesting. One of the first things I learned how to make are these “cut and paste” activities. They don’t take too long and I can customize them pretty quickly now that I have a template made. In addition, I like that it gives my class some practice cutting. The thing I had not anticipated, but love, is that they have learned how important it is to organize their answers before they start to glue them down. The first time we did one of these they were gluing too soon and regretting their choices. Now, however, they place the strips where they are pretty sure they belong, then double check everything before gluing them down. I love listening to the conversations they have when two people who sit beside each other aren’t sure if they have something right.

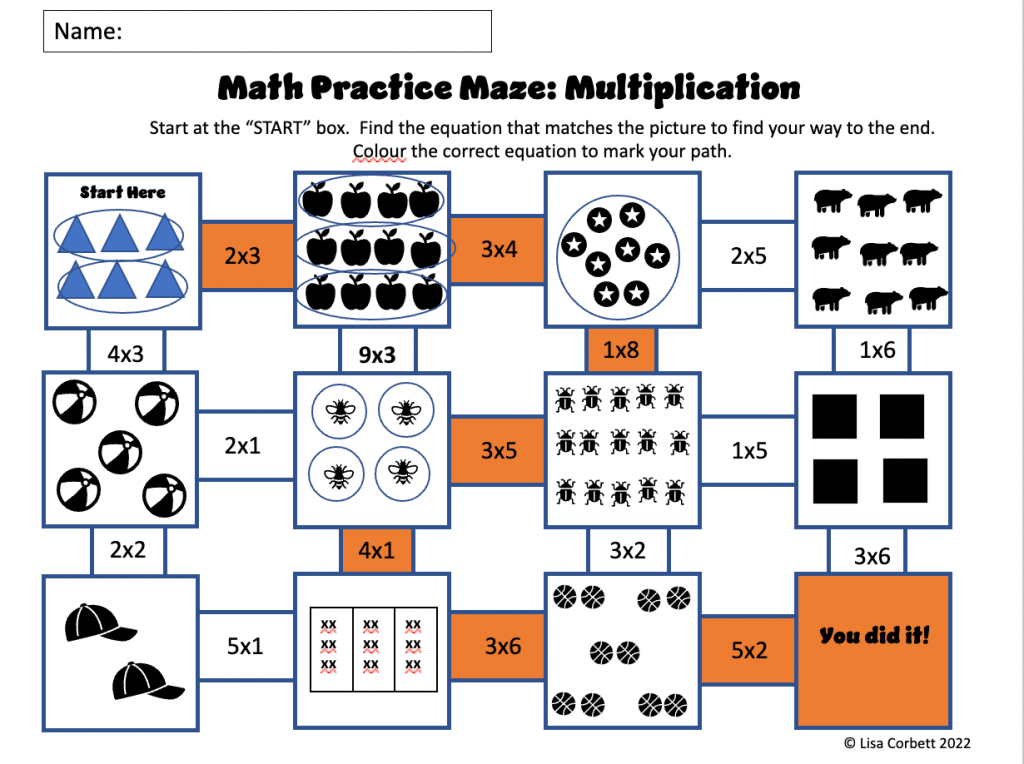
The next thing I learned how to make are these fun mazes. I have plastic covers that the papers slip into. I printed five of each maze style, then we passed them around all week for morning work. You’ll see some commonalities, so nobody was exactly sure which maze they were getting. They couldn’t fake their way through it! They had a great time doing them. They love using the dry erase markers to colour so this seemed fun to them. I have set these aside so that we can do them again in a few weeks for a review. Here is a picture of what it looks like when one is complete:

Speaking of reviews, the last thing I am posting today is a scavenger hunt. I think I mentioned in the money post that we LOVE LOVE LOVE scavenger hunts. I made this one as a review of all the things we have learned so far. It’s much more fun that doing worksheets for sure. Every child gets a recording sheet, copied front to back, and they wander around the room with clip boards looking for the equations they need to solve. I’ll definitely be making more of these reviews because it was so much fun. I was able to sit by one or two questions and observe every child as they came to that question. I have great notes! Most of them worked in self-selected pairs and they had great conversations about their strategies. I was initially thinking that 40 questions would be a lot and that we’d spend multiple days on this. I was prepared to shut it down if it was too much. However, they loved it. When I could see that some of them were more than 75% finished and others were less than 50%, I started observing them more closely. There were some students who were struggling with things we had left behind while working on multiplication. They had it while we were focused on it, but lost it when we moved on. That let me know that addition and subtraction need to be on constant repeat in our Number Talks, or in our morning work. This has definitely helped them.

We are moving on to division when we return after the holiday break, so I am already working on making my division worksheets, then it’s on to fractions.

multiplicationmazesDownload

multiplicationcutandpasteDownload

scavengerhuntreviewDownload

Show Me The Money!

I’ve been super busy.

That’s the only thing I can say. I’ve neglected the math blog once again. I think of it often, but never quite find the time to update.

I’ve got some spare time right now, so here it is. The update.

I’m teaching grade 3. I love it. Having a straight grade is so nice.

Now, on to other things. This summer I took a quick webinar about how to make my own math worksheets. (more info here) It was a lot of fun and now I am making them all the time! I’m going to start posting some here. The webinar was intended to teach people how to get started making and selling resources on Teacher’s Pay Teachers. I can’t be bothered with that. I have a lot of issues with that website and prefer to give away resources. I am adding a copyright, however, because I don’t want to find out someday that someone is selling my stuff on TPT.

Here is some stuff I made to use to teach my grade 3s about money.

We did this activity for the first time today. I put piles of fake money out (bills only today) around the room. I had a number label for each pile. Every child had a recording sheet. They went around the room finding the piles, counting the money and recording their total. I let them choose if they would work alone or with partners, and they did a little bit of both. Some people started with one partner then moved to another. I spent a lot of time watching and taking notes. We’ve done a number of these scavenger hunt activities at this point and they love them! I like to watch them help each other out, correct each other’s mistakes, and show each other the strategies they use. Today everyone was able to count the money without difficulty, and there were a few different strategies they shared. Sometimes they started by sorting the money into groups (e.g. put all the fives into piles of $10). Sometimes they had to count more than once to be sure.

On Monday, we are going to review the values of the coins, then we’ll repeat this with piles of coins. On Tuesday we’ll have mixed piles of coins and bills. (That’s assuming everything on Monday goes okay!) Finally, probably on Friday, we’ll have some more complicated piles with larger amounts. On that day I’ll most likely ask them to choose ten piles to count because sixteen will probably be too many. We’ll see!

I’ll be back soon with more of the things I’ve created. I like them and they’re working well.

You can download the recording sheet and labels for the piles here. I’ve also posted some cut and paste activities for counting coins. We haven’t used paste EVER in my class and I don’t think it’s even sold in stores anymore, but “paste continues to be what “cut and paste” remains in our lexicon so there you have it! Finally, I’m posting some word problems were’ going to work on in group using vertical nonpermanent surfaces, which you can read more about here.

money-counting-activity-1Download

word-problems-moneyDownload

coincutandglueDownload

Back in the groove

On Wednesday of this past week I realized I had gotten back into the groove of teaching math. I had been in it but fell out at some point. I knew I was not enjoying math and that I was feeling every day like I had missed the mark – the lesson was too easy, or it was too hard, or there were some interruptions that derailed us too easily. At some point I realized that there were so many different math strategies being used in the class that it was hard to have a conversation about our math. I decided that this week we would talk about all the strategies but we’d focus on making sure everyone could use a number line. We finished the Fosnot “Measuring for the Art Show” unit in about 3 days (should take more than that, and has typically taken me 10 days.) I decided to spend some time doing number strings and reinforcing the use of the number line to do it.

Here you can see we are using a lot of different strategies. Someone even suggested the traditional algorithm and several students knew how to use it. I’m crediting “at home learning” for that because this hasn’t happened in many years for me!

After two days of this, I asked everyone to complete three problems that I put on the board. They each have a whiteboard they were using to do this. “Do these three problems, and then you I want to take a photo of you and your work. Then you can clean up for lunch.” I thought that was good! But several of them were annoyed at ONLY being given 3 problems. I had to add more to the board. So, to recap, they wanted to do more math instead of get lunch.

I finally said, “Look, if you want to do this all day you could make up problems for each both er.” Then they spent the rest of the day making up problems for each other. A few of my friends weren’t sure what to do. I cancelled reading groups for two days to do math groups instead. By the end of that they knew how to add double digit numbers with the Base-10 Blocks and with the number line. We’ll get to the mental math eventually, but I needed to give them a few strategies to hang on to until then.

This week we’ll move on to another Fosnot unit called “Ages and Timelines” which has us focused more on subtraction, or rather “finding the difference” between two numbers. I feel like it will be a good fit for us.

I’m not sure if completing all of my math interviews would have helped. I still have a few to go (lots to go!) but what I already know about the class is that we are coming to the math from a variety of places. One of my small groups clearly knew what they were doing even though they had struggled with the first lesson and had given themselves a 😦 when I asked everyone to self assess. I asked them to explain.

Them: Well, I didn’t know this is what you meant.

Me: You don’t know I wanted you to add the numbers?

Them: No.

So, to recap, after two days of me saying “Add these numbers up.” They didn’t know what I meant. Like I said, we’re coming at this from a lit of different places. But I think we’ll mostly be in the same place, together, by the end of next week.

Baking

Are you still baking bread? At the beginning of the world-wide shutdown, everyone was baking bread and cookies and their own pizza. We are still doing this – we were doing this before. We’ve slowed down a bit because it’s been too hot to turn the oven on. But yesterday I made some bread and today my daughter is baking cookies.

She wants to do this all by herself. I have a recipe that’s meant to be easy for children to follow, and she has a lot of kitchen experience for a 9-year-old. She’s only needed help so far with the “1 slash 2 cup” of butter. We’ve talked about 1/2 dozens of times but it still eludes her. I showed her how to use the markings on the butter to figure out 1/2 of a cup. She then needed help with 1/2 cup of honey. Partway through pouring she realized she had the “1 slash 4” cup and thought it was going to be too much because she only needs “1 slash 2”. We’ve talked about this a bunch too, but in the moment she was confused again.  I coach her through it.  “1/4 is 1/2 of a 1/2.  So if you have 1/4, you have 1/2 of what you need.  So what do we need to do?”  She figures it out, I pour her another 1/4 cup of honey, and she’s back to working on her own.

I’ve been thinking a lot about baking and the learning that goes along with it. Little of it actually shows up in our curriculum. There’s problem solving, some collaboration (her brother doesn’t like chocolate so this is always part of our conversation when making cookies), communication, following instructions and, of course, measurement and fractions. At home this type of learning is very important to me. I want my children to head off to university with the ability to cook more than Kraft dinner, grilled cheese and scrambled eggs. The curriculum connections are a bonus. At school I cook or bake with my class maybe twice in a school year (less if there are students with allergies or special dietary needs in the class.)  I learned to cook at my grandma’s house, at my parent’s house, in Home Economics classes, and in neighbourhood 4H clubs.

If I was in charge of the curriculum, I’m not sure what I would eliminate in order to make space for cooking in the elementary grades.  I’m not sure there is anything we should exchange for cooking time. Secondary students still have the option of doing catering courses so they can learn to cook. Mostly I feel like learning to cook is part of how we pass our family and cultural traditions and values down to our own children.  I know some parents don’t teach their children to cook, but maybe that needs to be up to them.  Maybe this is one thing the schools have let go of for good reason. If I cook with my class it’s because we have a connection to something we’ve read about, or it’s a snow day and we need to fill the time with a worthwhile but fun activity.  I don’t feel compelled to teach them life skills like cooking or sewing.

 

 

Subtract

I know it’s only Tuesday, but I’m in a “celebrate the little things” frame of mind.  It’s helping me cope, which is pretty important for teachers under stress.  And other humans of course.

This week, only 2 days old, I am teaching area and perimeter.  But I like to continue with Number Talks even when we’ve moved away from the computation portion of our work. Yesterday I started with one from Sherry Parish’s “Number Talks: Whole Number Computation” book. I chose one from the grade 2 section:  20-19, 20-14, 20-12.  We talked about how we could use all of our strategies from the math wall, but that counting up seems to work better than counting down.  We used the math racks for this activity, and I celebrated my own ability to say “subtract” every time instead of reading the problem as 20 TAKE AWAY 14.

Then today, we started with 20-19 (because one thing I have definitely learned from Cathy Fosnot and her Number String work is that starting with a helper problem is very important – this is not part of the Number Talks book work.)  Everyone remembered or quickly figured out that the answer is 1.  Then I wrote 30-19.  They weren’t so sure at first.  It took us a while to get to 11.  Some kids wanted to count all the way down (their go-to strategy).  Some wanted a math rack so I pointed out it doesn’t have 30 beads so what would they do, they didn’t have a plan. Some made random guesses AS ONE DOES!  We started to talk about our potential answers.  I purposely called on a student that I knew had the right answer AND that I knew could explain the thinking to share.  This child did a great job of noting that the helper problem was helpful.  If we think about how 30 is just 10 more than 20, but we still subtracted 19 then the answer should be 11, or 10 more than 1. I pulled out the math racks. I showed them 30-19 using a 20 rack and a 10 rack.  This way I could show how I added 10 more in but didn’t remove any more than I had the first time, leaving 10 more remaining after I “took away” or “removed” the 19 beads on the rack. After we did 40-19, someone noticed a pattern.  This is honestly the thing that makes me happiest sometimes.  Some groups of kids will notice patterns right away and then stop puzzling over the math because they have found the short cut.  But this class always takes a bit longer to see the pattern.  It’s fine with me, because we have a lot of good conversations along the way.  But I’m also glad when the pattern becomes part of our conversation too.  Even after this child thoroughly explained the pattern, some were skeptical.

Along the way I was drawing the number lines.  I decided to draw a new one each time because I wanted them to clearly see how each time the 19 didn’t change, but our starting and ending point did.  I also wanted to highlight the iterated units.

We talked about each of our strategies:  does it make sense to count up?  to count down?  to try and “take away” something?  to think of an addition problem that would help?

Two weeks ago I blogged about a moment when everyone was working independently.  It has rarely happened since. But it is happening, throughout our day.  Slowly but surely we are edging forward, and today’s math was a reminder to me that we are indeed doing good work. Not every day is easy.  In fact, today wasn’t that easy.  But this was my shining moment.

We’ll continue on with this tomorrow, but I will use some other number besides 19.  I am also going to write out today’s work on a chart paper because I think it will help us going forward and, therefore, deserves a spot on the math wall.

Subtraction

What does “-” mean in math? As in 5-2=

We had an excellent conversation about this during a Number String this week. I went off script after discovering that some of my friends didn’t know how (as in “no idea” how) to subtract 23 T-Shirts from their inventory in our math lesson.

This is what we decided:

The next day we talked more about “take away” using the math rack. Then we talked about how we can count back on a number line. Then we talked about how we can actually count up on a number line in order to find the space, or difference, between 2 numbers. One friend was very keen to keep explaining how adding and subtracting are opposites, and during one explanation solidified his own understanding of how he uses what he knows about adding to subtract.

I had my strings planned out for the week, but on Wednesday I realized we actually needed to do something different than planned. Literally everyone in grade 3 is doing well adding double digit numbers. They need more practice for sure, but the Strings were not moving us forward. At the same time a weaker skill (from way back in grade 1) popped up and I felt it was a good time to address it.

I’m thinking more and more and more about how math learning happens on a developmental continuum. Everyone travels along the continuum at a different pace. Hopefully nobody dawdles in one place for too long, and hopefully they remember what they’ve learned. I’m confident everyone has past experience with subtraction. However, for some reason, it didn’t stick. It’s for this very reason I had my grade 2’s dawdling in their own spot on the Landscape of Learning all week. They played games that had them practicing addition facts, and started creating their own flash cards to take home and practice. Next week they’ll be doing the same with subtraction facts.

Snow Day Math: Data Management

We had our first Inclement Weather Day on Friday, November 1.  In my school, and I think this is true in many schools around here, we double up classes on a snow day.  Few children come those days and it’s a great chance for kids to try things out in another room, see old friends, and get to know or reacquaint themselves with a new teacher.  For a teacher it’s a great chance to get caught up on things. I worked on some necessary paperwork that has been bugging me. The teacher I partnered up with did some Running Records.

For the last 80 minutes of our day, my teaching partner and I had the students together.  We decided to have them gather data this year on Snow Days.  We wondered how many children were in the school that day, and what kind of information we could get from the numbers.  We sent teams of students to each classroom to ask how many students were in each homeroom that day. We then gathered together and reported our data.  We organized it all on a chart.  We had a great discussion about the numbers:  Which class had the most students? Which class had the least?  Which classes had the same?  We wondered if the numbers will stay the same for every snow day.  Were the numbers smaller than usual because it was the first snow day and the day after Halloween? We noticed that some of the older classes didn’t have many children in them and the younger classes generally had more.

We even calculated the total number of students in the school. My grade 3 students were able to do this!!  We had a great conversation about a strategy for adding up 20 numbers.  I think they’ll be able to do this independently next time…or nearly independently anyway.  I suppose that depends on how long we wait until the next inclement weather day.  I’m thinking now that we should figure out what percentage of the student population came that day.  We were a group of grade 1, 2 and 3 students, so percentages are above our curriculum expectations. However, I bet I can procrastinate house keeping for a few more hours by figuring out how to make some circle graphs of this data.  They should certainly be able to read those.

Our plan is to do this every time we have a snow day, then compare the data over a long period of time.  I wonder what trends we will see!   I’m excited to share this data with the children who were not in school on Friday and see what they notice about the data.

Number Strings/Number Talks

Math was fine this week. We started doing more place value work while working on “The T-Shirt Factory” Context for Learning unit by Cathy Fosnot. It’s always an interesting one, but I actually didn’t do it with my class last year.  We weren’t ready for it until much later than this and when we were ready for it…I forget what we did instead.

This week was Halloween. That means an interrupted day on Thursday because of the Halloween Parade.  I anticipated a day of difficulty on Friday as well, and while we’re at it, let’s just admit that Wednesday wasn’t going to be easy either.  See how hard it is to stay on schedule?  That’s why we didn’t exactly stay on schedule with the unit.  However, I didn’t skip math any of those days – even the snow day on Friday!

I did a fun mapping activity with a Halloween theme one day when I was pulled out for a meeting, and we did a lot of work with the base ten blocks.  But every single day I made sure that we were doing a Number Talk.

During a Fosnot unit, there will be a lot of Number Strings.  But when I am not teaching a specific skill and want to review things that I hope everyone already knows or that I know they need to practice, I go back to Number Talks.  This week we used some from the Grade 2 section of the book “Number Talks” by Sherry Parish.  We started with single digit numbers and I found out on day one that most everyone understands commutative property.  I repeated a talk that would reinforce this with double digit numbers on the second day.  On Wednesday, Thursday and Friday we talked about the “doubles plus 1/doubles minus 1” strategy.  These strategies are now displayed on our math wall so we can refer to them often.

This week, I am doing Number Strings to support the learning in the unit.  Because I can barely remember what day it is on most days I have to write my numbers on a Post-it note.  These will sit on my lap top all week or I will lose them.  I find it also has me thinking many times during the day about what we are doing in math, which is good for my brain.

Some of these are from the unit and some are from my head.  I know my learners well enough at this point that I’m sure we will need to do practice the skills that are in these strings multiple times.  They’ll be practicing them while doing the work in the unit as well.

I’m going to finish off my planning today by making my anecdotal record sheet for this unit.  (Just double checked and I already made one a few years ago! WOOHOO!

This week we did…something

It was a weird week for math. I spent some counting routine time counting backwards. They’re pretty good at it. I thought they could be independent as a small group while I worked with some people on something else. I was mistaken. We’ve still got some social collaboration and problem solving things to sort out. That’s the thing I’m reflecting on most as I move forward into next week. I know where I’m going lesson wise, but am still sorting through some of the mathematical process teaching I need to do.

Because of the work I’m doing to spiral in math this year I am feeling like I don’t have a lot of things to use for comments on progress reports. I’ve decided to focus my commenting on some of the mathematical process skills.

This week I’m realizing that so far I’m doing a lot of the selecting when it comes to the tools we use. I put a lot of work into making sure everyone knows how to use the tools properly. Now it’s time for me to talk about how the tools have specific purposes for which they are best suited. We can’t always choose the colour tiles because we like how they stack! It’s time to move along and choose based on what each tool helps us understand. I’m doing some guided math rotations this week, and want to come up with some opportunities for kids to articulate why they chose a certain tool.

That is going to lead us to some communication work. We’re doing okay with this when I am poking and prodding. Now it’s time for the students to think about being really clear with their communication. I’m going to jump in and set up a FlipGrid they can use to explain something they’ve done. They’ll have to think about how to make me understand their thinking when I watch the video at home (cause you know I’ll never find time or a quiet spot where I can view these at school!)

Finally…actually, I’m going to stop there. Don’t need to set too many goals at once, right? I’m also diving into “The T-shirt Factory” Context for Learning unit with my grade 3s and we’ll need to be focused on that math at the same time. Not totally sure what my grade 2s will do next week, but I’m sure I’ll get it sorted out.

It’s important to have a focus on teaching and doing math. But the seven processes are an important part of that we can’t neglect. In a problem solving based classroom students need to be able to do more than accurately find answers.

Making 10

You know when something goes so well on Tuesday that you assume Wednesday is going to be a piece of cake and then on Wednesday everything goes so wrong that you have to stand back and ask, “What was THAT?”  Well, that was my Wednesday.

On Monday we made groups of 10 to count totals of stuff.  I took pictures.  We congressed and talked about how efficient it is to count groups of ten.

On Tuesday we made groups of 10 and then created a chart where we recorded how many groups of 10 we had, how many loose (ones…the singles that didn’t make a group of 10) and noticed how those related to the number I wrote down for the total.  I was blinded by all the lightbulbs going off over the heads!  We ended the day with a fun writing activity. I had a number which I flashed to everyone.  They had a white board and they had to recreate our chart.  If I showed 47, they had to write “4 tens, 7 loose = 47”  but in a chart that I don’t  have a picture of.

On Wednesday we counted stuff and I asked them how many they would need so that there would only be groups of ten – no loose, or single, items. It was a disaster.  Kids were doing all sorts of things but making groups of 10 was not one of them. Figuring out how many more they would need was also not one of them.

On Thursday I took a step back. Or maybe sideways. I had some great counting items from the resource centre.  I had bowls to put them in, which meant that everyone had somewhere around 50 items, which was a manageable number for everyone.  I started by showing them a math rack with 5 red beads slid to one side. “How many would I need to slide over so that I would have 10 beads on this side?”  They got it easily.  Then I pushed 10 over and asked how many I would need to have 20.  Then I did 15, and asked about 20.  Then I did 7 and asked how many would I need to push over to have 10.  I repeated with a few more numbers – if I had 8 how many would I need?  What if I had 12?  or 18? Then I handed out the bowls and everyone made piles of 10 and I asked them how many they’d need to have only piles of 10.  And they could tell me. I took pictures so we could discuss as a group. I am happy to report that THEY GET IT!  Then we played “Tens Go Fish” and all was right in the world.

My family will be driving for the holiday weekend, so I may not end up posting about Friday.  But my plan is to do a bunch of backward counting.  We have a holiday on Monday and I am away on Tuesday so I don’t want to move forward with the next lesson in the “Collecting and Organizing” Context for Learning unit.  We haven’t done any backward counting, so this seems like a good way to spend our math time tomorrow.

I’m wondering at this point of working with a new tool was actually part of the key to this success.  We have done a lot of work with my counting jars, and I think they already know the answers for many of these jars.  They remember that there are 8 bottle caps in one jar, and 47 beads in another.  Are they really thinking about these numbers still?  Or are they just sort of multi-tasking – half paying attention the materials and the piles of ten while also thinking about Minecraft? I feel like having a new item to count got them thinking about the counting again.

Another interesting thing happened on Thursday.  A child who keeps telling me that grade 3 is too hard listened to me give the instructions for “Tens Go Fish”. As I neared the end he got excited. “Madame!  I played this game last year with Madame G!”  It was the most enthusiastic I have seen him in math.  Making that connection to the familiar was so important for him! Was the game maybe too simple for most grade 3 students?  Yes.  Was it still useful? I think so.  They could think about this in a different way as grade 3s than they had as grade 2s. They are now pretty proficient with making tens, for the most part anyway, so this really was a practice.  But they are now thinking about how making tens is useful for problems like 32+18, or 17+13.  Next, the grade 3s are moving on to triple digit numbers, and I feel excited about what this will mean for their understanding.